The relative strength of topological graph colouring obstructions

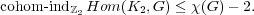
The following is a summary of a talk I have given at the combinatorics workshop in Oberwolfach in January 2006. This work has subsequently grown into the article Graph colourings, spaces of edges and spaces of circuits.

Extended abstract

In the proof of Kneser’s Conjecture, Lovász has shown that if the neighbourhood complex of a graph G is (k - 1)-connected, its chromatic number is at least k+2. Later formulations of this theorem replace the neighbourhood complex by the complex Hom(K₂,G), which is homotopy equivalent to it. One variant of this theorem is the following.

Theorem 1 [Lov78, BK06a]. Let G be a graph with at least one edge. Then

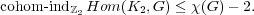
For graphs H and G, the cell complex Hom(H,G) has the graph homomorphisms from H to G as 0-cells, while the higher dimensional cells are indexed by multi-homomorphisms, functions which assign to every vertex of H a non-empty set of vertices of G such that every choice of one of these for every vertex of H yields a graph homomorphism. An involution on H which flips an edge makes Hom(H,G) into a free ℤ₂-space. The emphasis on the cohomological index of the ℤ₂-action comes from the work of Babson & Kozlov on the following theorem which proves a conjecture by Lovász.

Theorem 2 [BK06b, Sch05]. Let G be a graph with an odd cycle and r ≥ 1. Then

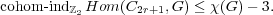
Previous proofs of this theorem can be summarized at follows. One studies the complex Hom(C_2r+1,K_n). This is the hard part. Then the functorality of Hom in the second argument is used to deduce information on Hom(C_2r+1,G) from the existence of an n-colouring of G, i.e. from Hom(G,K_n)∅.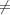

Extending a surprising and elegant partial proof of Theorem 2 by Živaljević [Živ05a, Živ05b], we present a simpler way of obtaining the desired information on Hom(C_2r+1,K_n), or even Hom(C_2r+1,G) for an arbitrary graph G. This uses the idea that Hom is not only functorial, but that there is a continuous map extending composition of homomorphisms, in this case

Using properties of this map and of the ℤ₂-actions on Hom(K₂,C_2r+1) induced by involutions on K₂ and C_2r+1 we obtain the following result.

Theorem 3. Let G be a graph with an odd cycle and r ≥ 1. Then

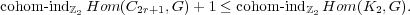
This reduces Theorem 2 to Theorem 1. It therefore proves Theorem 2 in a simple way, but also shows that lower bounds on the chromatic number that can be obtained from it can also be obtained from the complex Hom(K₂,G) originally studied by Lovász.

Theorem 3 can be generalized as follows.

Theorem 4. Let G,G′ be graphs with involutions, the involution on G flipping an edge, and k ≥ 1. If

• coind_ℤ2 Hom(G,G′^ℤ₂) ≥ k - 1,
• there is a graph homomorphism from G to G′ that commutes with the involutions, and
• Hom(G,G′) is (k - 1)-connected,

then

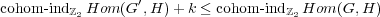
Here, G′^ℤ₂ is a graph whose vertex set is the set of all orbits of the involution on G′. Its edge set is the largest one such that the map V (G′^ℤ₂) →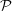(V (G′)) assigning to each orbit the orbit itself is a multi-homomorphism.

This theorem can be applied to yield a result analogous to Theorem 2, with circuits of chromatic number 3 replaced by Kneser graphs of chromatic number 4.

References